位运算的性质和使用
机器数的表示
在我的Java学习笔记第四篇《进制和数学数算》中,简单地提到了计算机三码运算的过程。数据在计算机中的形式称为机器数,其表示方式可以有四种:原码表示、反码表示、补码表示、移码表示。
用8位二进制数比较各码值的区别
| 十进制 | 二进制原码表示 | 二进制反码表示 | 二进制补码表示 | 二进制移码表示 |
|---|---|---|---|---|
| 127 | 01111111 | 01111111 | 0111 1111 | 11111111 |
| 126 | 01111110 | 01111110 | 01111110 | 11111110 |
| …… | …… | …… | …… | …… |
| 1 | 00000001 | 00000001 | 00000001 | 10000001 |
| 0 | 00000000 | 00000000 | 00000000 | 10000000 |
| -0 | 10000000 | 11111111 | 00000000 | 10000000 |
| -1 | 1000 0001 | 11111110 | 11111111 | 01111111 |
| -2 | 10000010 | 11111101 | 11111110 | 01111110 |
| -3 | 10000011 | 11111100 | 11111101 | 01111101 |
| …… | …… | …… | …… | …… |
| -127 | 11111111 | 10000000 | 10000001 | 00000001 |
| -128 | 无法表示 | 无法表示 | 10000000 | 00000000 |
原码:按照数字的绝对值用二进制表示,符号位用 0 表示正数,1 表示负数。原码是二进制表示中最简单的形式,但存在+0和-0的不同。
补码:原码保留符号位,其他位取反后+1,位运算相反数公式 -x = ~x + 1。补码解决了0问题,并且能表示整数最小值。在Java中可以通过Integer.toBinaryString 方法得到。
移码:把负数绝对值的二进制表示取反,然后再加上一个偏移值(offset)。可以直接通过码值大小来确定真值大小
小数的表示方式
浮点数普遍使用IEEE 754工业标准,约定对于32位单精度浮点数,符号位S为1位,阶码长度(指数位E)为8位,尾数长度(分数位N)为23位
如上图要计算小数0.15625的二进制码,首先要把 0.15625 转换成二进制数 0.00101 ,然后小数点右移成为 1.01×2^−3 。因此阶码-3用移码表示,因此阶码为(移位值为127,即用 127+(−3)=124 的二进制值来表示-3) 0111 1100 ;尾数为 010 0000 0000 0000 0000 0000 。
float格式可以表示的最大正数 (-1)^0 2^(254-127) (2-2^-23) ≈ 3.4 * 10^38
补码运算的本质
前段时间在B站学习了视频《这个你没听说过的数字系统,能够解决数学中最困难的问题》,里面提到“无限位数字”的概念,这和“舍弃溢出的符号位实现加减运算”这一概念具有相同逻辑性。
十进制负数转二进制:①整体取反②减1后转二进制③整体取反
二进制负数转十进制:①整体取反②加1后转十进制③整体取反
[+001]补=00000001,[-001]补=11111111
[+127]补=01111111,[-127]补=10000001
[+045]补=00101101,[-045]补=11010011
上述运算的本质,是二进制数+1后可以向上传递进位,然后抛弃掉溢出的符号位。类似于钟表,往后拨两个小时和往前拨10个小时是一样的,加一是因为还有一位0。
减法运算就是被减数加上减数的补码,而十进制减法运算8 - 7可以转换为8 + (-10 + 3),二进制也可以用“比减数高一位的一个计数单位减去减数来得到将来要用到加法里面的加数”,而二进制里用高一位的一个计数单位减去正数的补码就相当于绝对值按位求反再末尾加1!!!例如
-1可以表示为(10000001)₂除符号位外取反加一(11111110+1)₂得到(11111111)₂,也可以表示为(10000000 - 00000001)₂得到的(11111111)₂
掌握这个本质就可以直接用原码进行计算了
10-1=(00001010-00000001)₂=(00001001)₂=9
10+(-1)=(00001010+11111111)₂=(100001001)₂,高位溢出直接不要了,就变成(00001001)₂=9
位运算的使用
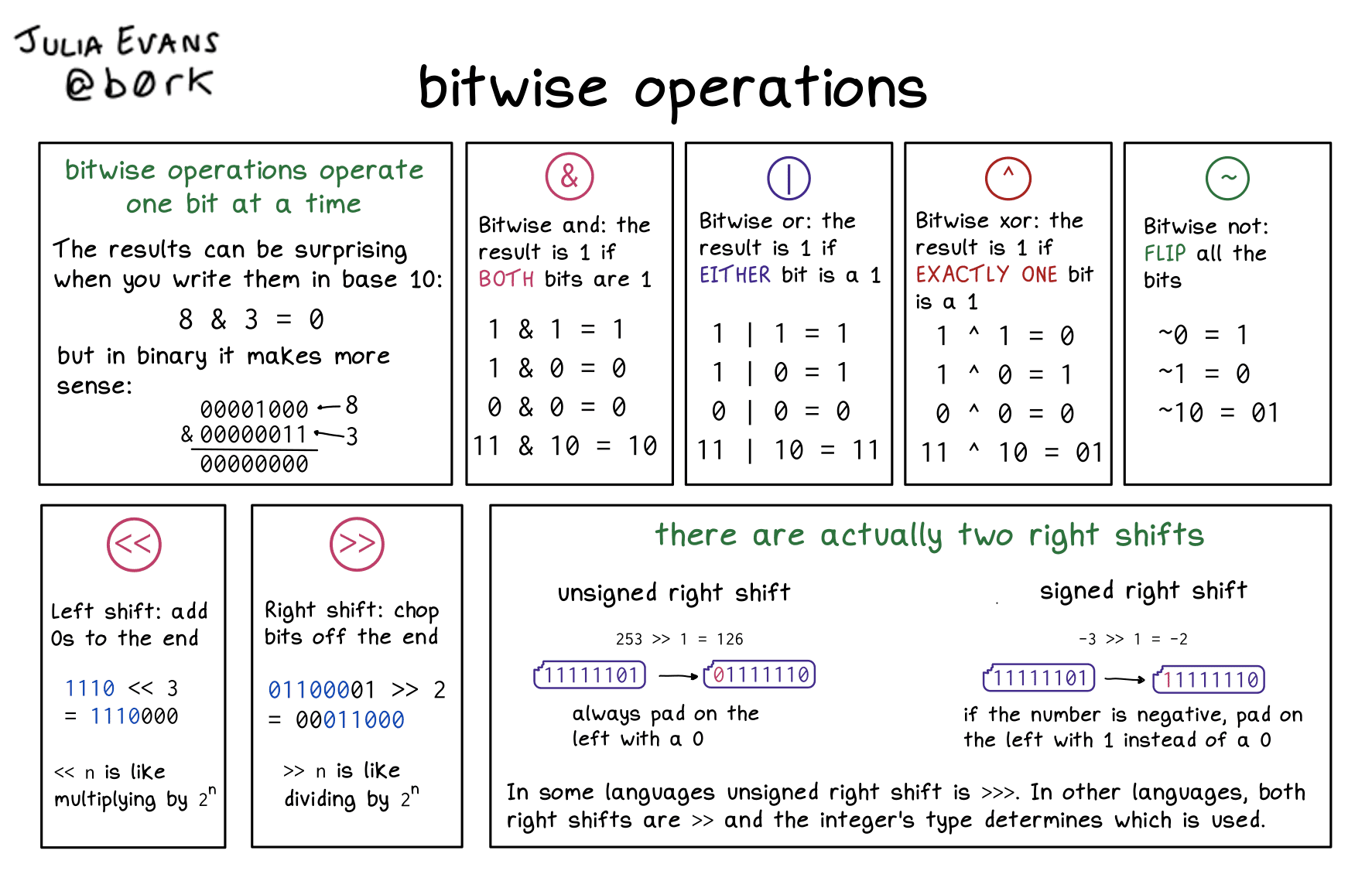
位运算的运算规则如下:
| 符号 | 描述 | 运算规则 | |
|---|---|---|---|
| & | 与AND | 两个位都为1时,结果才为1 | |
| \ | 或OR | 两个位都为0时,结果才为0 | |
| ^ | 异或XOR | 两个位相同为0,相异为1 | |
| ~ | 取反NOT | 0变1,1变0 | |
| << | 左移SHL | 各二进位全部左移若干位,高位丢弃,低位补0 | |
| >> | 右移SHR | 各二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移) |
图片出处:bitwise operations (wizardzines.com)
~x = -x - 1:0与-1,1与-2,2与-3……等等。因此,该性质是not操作中最常使用的性质。
(~x)&x = 0:任意数与它的取反数的and操作结果为0。
(~x)|x = -1:任意数与它的取反数的or操作结果为-1。
(~x)^x = -1:任意数与它的取反数的xor操作结果为-1。
x|0 = x:任意数x与0的or操作结果为x自己。
x^0 = x:任意数x与0的xor操作结果为x自己。
x^y^y = x:任意数x与任意数y进行两次xor操作结果为x自己。
AND操作(&)
判断奇偶数:
x & 1 == 1。(注意:这样的逻辑会把0当作偶数,注意设置条件判断)判断第n个二进制位是否为1:
(x & (1 << n) != 0去掉低位的1
x & (x-1)按字节读取
byte & 0xff,清除字节的高位,将其转换为无符号值。用于在网络编程、文件IO或加密解密等场景中处理二进制数据计算二进制中1的个数(见下方“单数字运算”代码)
OR操作(|)
- 生成组合编码,进行状态压缩
- 在加密或编码中,将两个字节合并
XOR操作(^)
两个整数交换变量名:注意数组的某个下标的值,执行按位异或后将会变0丢失原数据
1
2
3
4
5
6public static int[] swap(int a, int b) {
b ^= a; // b = b ^ a
a ^= b; // a = a ^ b, 此时 a = (a ^ b) ^ a = b
b ^= a; // b = b ^ a, 此时 b = (b ^ a) ^ b = a
return new int[]{a, b}; // 返回交换后的结果
}数据判重:连续的xor操作会自行抵销了出现了偶数次的数,剩下的就是不重复的数。经典算法题:Single Number、Single Number II、Single Number III、Missing Number
数据加密:利用x^y^y = x的性质,可以在使用相同的密钥(私钥)的情况下做一个简单的对称加密,实现将字符串“我爱你”加密为“抺犚俋”(密钥为0xAB),也可以用此密钥对加密后的字符串再进行一次异或运算还原出“我爱你”(注意:简单的异或加密并不是安全的加密方式,它仅提供了基本的混淆。在实际应用中,为了更安全地加密数据,应该使用专门设计的加密算法,如AES、DES等。)
1
2
3
4
5
6
7
8
9
10
11public class Test02 {
public static void main(String[] args) {
String s = "我爱你";
int key = 0xAB;
String temp = "";
for(int i = 0, len = s.length(); i < len; i++) {
temp += (char)(s.charAt(i) ^ key);
}
System.out.println(temp);
}
}
SHL操作(<<)
- 求某个数和2的n次方乘积
x << n - 注意算数左移会导致高位符号溢出,可能将负数变成很大的正数
- 经典算法题:Power of Two、Power of Four、Binary Number with Alternating Bits
SHR操作(>>)
- 求某个数和2的n次方的模
x >> n,因为保留符号位,所以对正数负数都能用 - 求平均值:为防止溢出,一般使用无符号右移Unsigned Shift Right(>>>)
(a + b) >>> 1
二进制位存储数据
重要的是分治和移位思想。补充阅读:二进制与位运算实用操作汇总(实战篇) - 知乎 (zhihu.com)
单数字运算
二进制码可以看作是多个布尔值的集合,因此一个int类型的值可以存放32个只有0/1值的字段。假设一个网站注册时要用户勾选感兴趣的类目,一共有8项。那么这时,就能用一个byte值去表示所有的可能性组合:
1 | //定义一个保存用户选项的变量 |
添加元素
1 | //假设选中了item2,5,7,8 |
访问元素
1 | if ((option & item1) != 0) System.out.println("item1 被选中"); |
删除元素
1 | //and目标的取反,仅会影响 option 中与 item5 和 item8 对应的位。其他位的数值保持不变。 |
反选元素
1 | option = ~option; |
删除最小元素
1 | option &= option - 1;//将最右侧的1设置成0 |
求集合大小
本质上就是统计二进制数中1的个数,就是多次求出最末端的1
1
2
3
4
5
6
7public static int count(int n) {
int r = 0;
while(n) {
n &= (n - 1);
++r;
}
}纯位运算方法,可以更快解决
1
2
3
4
5x = option & 0xFF;//只保留 option 的最低8位,将高位都设为0。
x = (x & 0x55) + ((x >> 1) & 0x55);//对 x 的低4位进行位运算。它提取奇数位(位置1、3、5、7),并将它们与偶数位(向右移动1位)相加。常数 0x55 用于屏蔽和分离这些位。
x = (x & 0x33) + ((x >> 2) & 0x33);//每4个二进制数计算1的个数
x = (x & 0x0F) + ((x >> 4) & 0x0F);//每8个二进制数统计1
集合间的运算
1 | //重新定义3个集合 |
经典算法题:Subsets、Maximum Product of Word Lengths、Letter Case Permutation、Repeated DNA Sequences
位集
用bit组成的数组来存放值,用bit状态1、0代表存在、不存在,取值和存值操作都用位运算
限制是必须为连续范围且不能过大。好处是极大的节省空间,因为1个数字只占用1个bit的空间
参考视频资料:算法讲解032【必备】位图,练习题:Design Bitset - LeetCode